Las Preguntas más Comunes en SAT Math – Advanced Math (Parte 2)
Domina temas frecuentes en Advanced Math: Funciones, interceptos, máximos y mínimos
Por Maru Berríos, Coach de SAT/PAA, Fundadora y Directora de Honors Learning Center, líder en tutorías en Puerto Rico con más de 30 años de experiencia.
La sección de Advanced Math en el SAT se enfoca en destrezas necesarias para cursos más avanzados — como Precálculo y Cálculo.
Aunque a primera vista esta parte del examen puede parecer intimidante, lo cierto es que también es bastante predecible. Muchos de los temas que se repiten no son complejos, y una vez los reconoces, sabrás exactamente qué hacer.
¿Qué tipo de preguntas veremos en la Parte 2?
En esta segunda parte de la serie, trabajaremos con ejemplos de preguntas típicas de Advanced Math relacionadas con funciones:
🎯 Hallar el valor de f(x)
🎯 Hallar los interceptos
🎯 Hallar máximos o mínimos
Cada ejemplo incluirá dos métodos:
🧮 Uno paso a paso con álgebra tradicional
Uno usando la calculadora Desmos, integrada al SAT digital
Este artículo no cubre todas las preguntas posibles de Advanced Math — pero sí te presenta una guía práctica con los estilos de pregunta que más se repiten en el SAT. Verás ejemplos paso a paso, estrategias para resolverlos y cómo usar Desmos SAT como herramienta de apoyo.
📘 ¿Te perdiste la Parte 1?
Ahí repasamos las preguntas más comunes de Álgebra en SAT Math.
👉 Haz clic aquí para leerla.
🧠 ¿Qué es una función?
Una función es simplemente una ecuación donde y se escribe como f(x) para destacar que depende de x. Es una notación diferente, una forma distinta de decir lo mismo.
Por ejemplo:
ecuación: y = 3x + 5
función: f(x) = 3x + 5
En otras palabras: f(x) = y
Si te asustas cada vez que ves un f(x), recuerda que se refieren a y. ¡Es lo mismo!
Veamos cómo luce una pregunta típica con el uso de f(x) en el SAT.
🎯 Preguntas Comunes SAT Math: Encontrar el valor de f(x)
En esta pregunta típica del SAT, te piden evaluar una función para un valor específico. Es decir, sustituir ese valor en la función y calcular el resultado.
🧠 ¿Qué significa f(2)?
Hallar el valor de y cuando x = 2.
Recuerda que f(x) no es otra cosa que y. Así que: f(2) = y cuando x = 2.
🧮 Con Álgebra
Para encontrar el valor de f(2) en la función, simplemente sustituimos x = 2 en la función:
El valor de f(2) es 17. La contestación correcta es la alternativa C.
Con Desmos
- Escribe la función tal cual como te la dieron.
- En la próxima línea, escribe f(2), que es precisamente lo que te están pidiendo.
- Desmos te dará la respuesta en la misma línea.
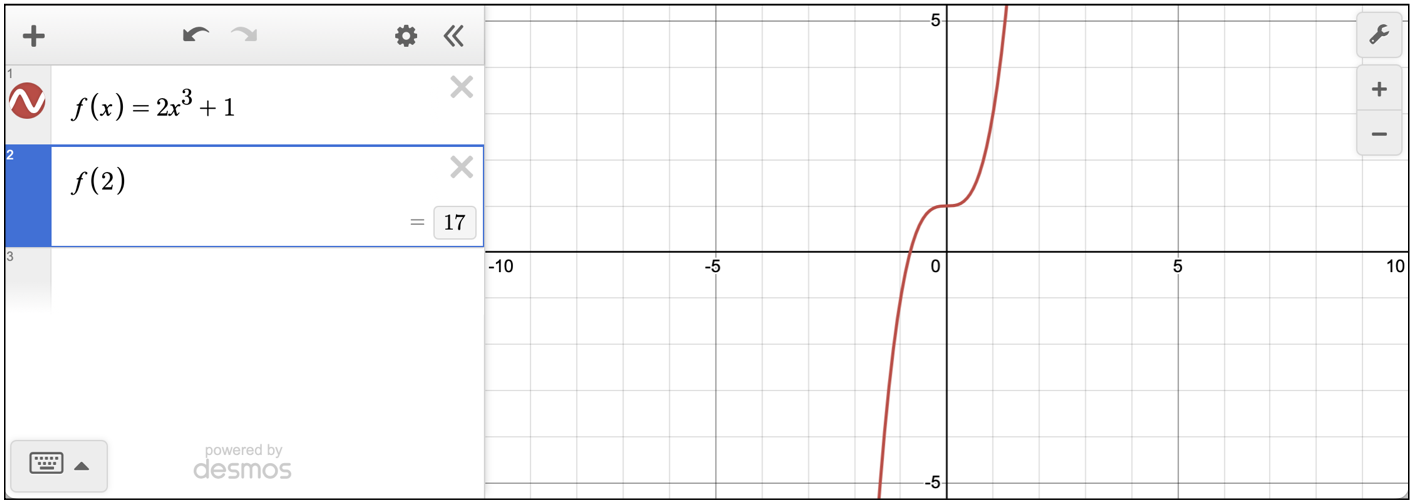
La contestación correcta es 17, la alternativa C.
💡 Recuerda:
f(x) = y
Cuando te preguntan por f(2), están pidiéndote el valor de y (el valor de la función) cuando x = 2.
👉 f(2) = y cuando x = 2.
⚠️ Cuidado:
No confundas f(2) con multiplicar la f por 2. ¡No es f · 2!
Es solo una notación formal para decir que vas a sustituir x = 2 en la función.
🧠 SAT Tip:
Usa Desmos para evitar errores de cálculo.
Pueden costarte la pregunta.
🎯 Preguntas Comunes SAT Math: Encontrar interceptos en funciones
Otra de las preguntas más frecuentes en SAT Math es una como esta:
🧮 Con Álgebra
Para resolver, recuerda que el intercepto en y es una coordenada, (x, y), pero en este caso te la presentan como (0, b). Esto significa que:
(x, y) = (0, b)
x = 0 y = b
En otras palabras, el intercepto en y ocurre cuando x = 0.
Para encontrar b, basta con sustituir x = 0 en la ecuación dada.
Puedes cambiar f(x) por y sin problemas, ya que ambos representan lo mismo:
La contestación correcta es -15.
Con Desmos
- Escribe la ecuación original tal como aparece en la pregunta.
- Observa la gráfica: vas a ver una curva en forma de U — una parábola.
- Haz clic en el punto donde la parábola cruza el eje de y — el intercepto en y.
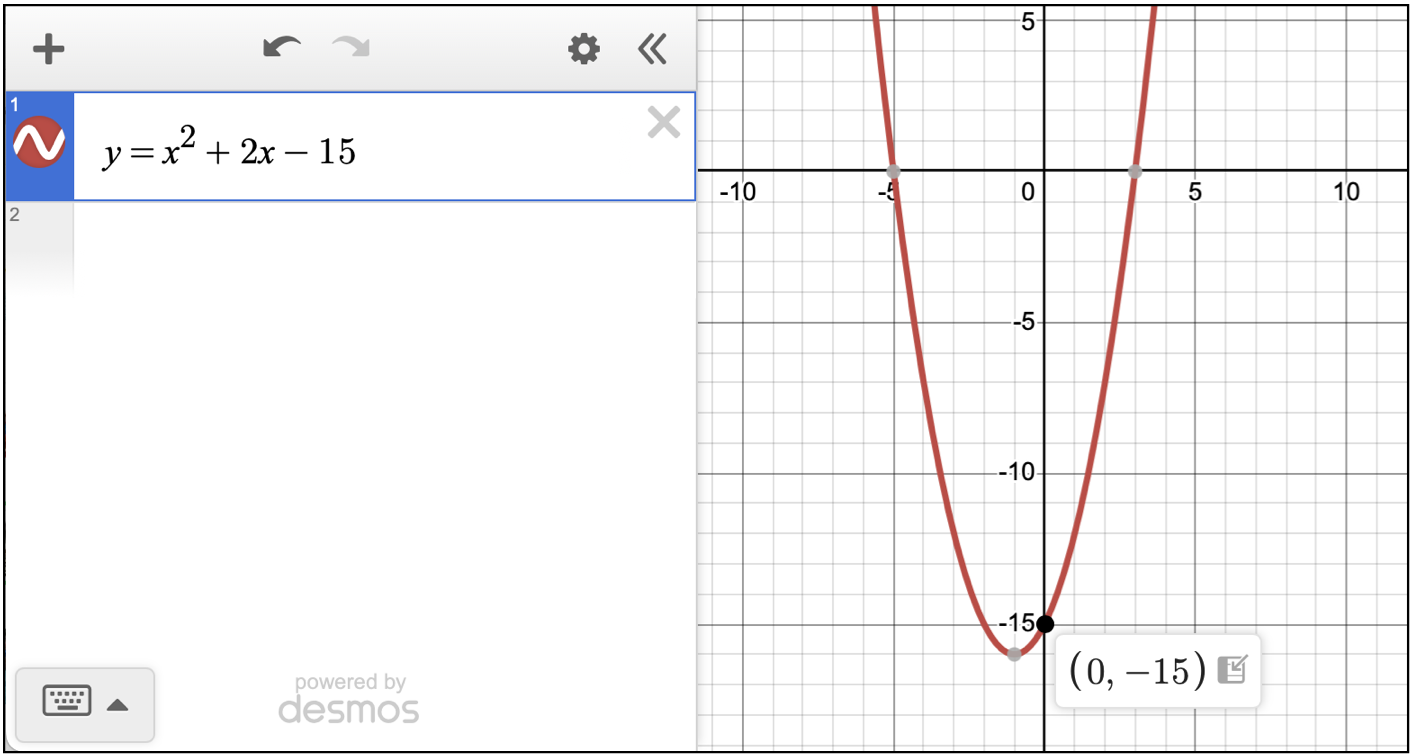
Eso significa que b = -15. La contestación correcta es -15.
Si te pidieran un intercepto en x, el procedimiento es similar al del intercepto en y.
Veamos:
🧮 Con Álgebra
Para encontrar un intercepto en x, recuerda que el punto estará en el eje de x, y por lo tanto f(x) = 0. Puedes sustituir f(x) = 0 en la función dada y resolver para x:
x − 5 = 0
x = 5
Esto nos da los valores x = -15 y x = 5, lo que indica que la gráfica interseca el eje de x en dos puntos.
Como la pregunta dice “an x-intercept”, no están pidiendo los dos, sino uno de ellos.
La contestación correcta es (-15, 0), la alternativa A.
Con Desmos
- Escribe la ecuación original tal como aparece en la pregunta.
- Haz clic en los puntos donde la parábola cruza el eje de x (los interceptos en x).
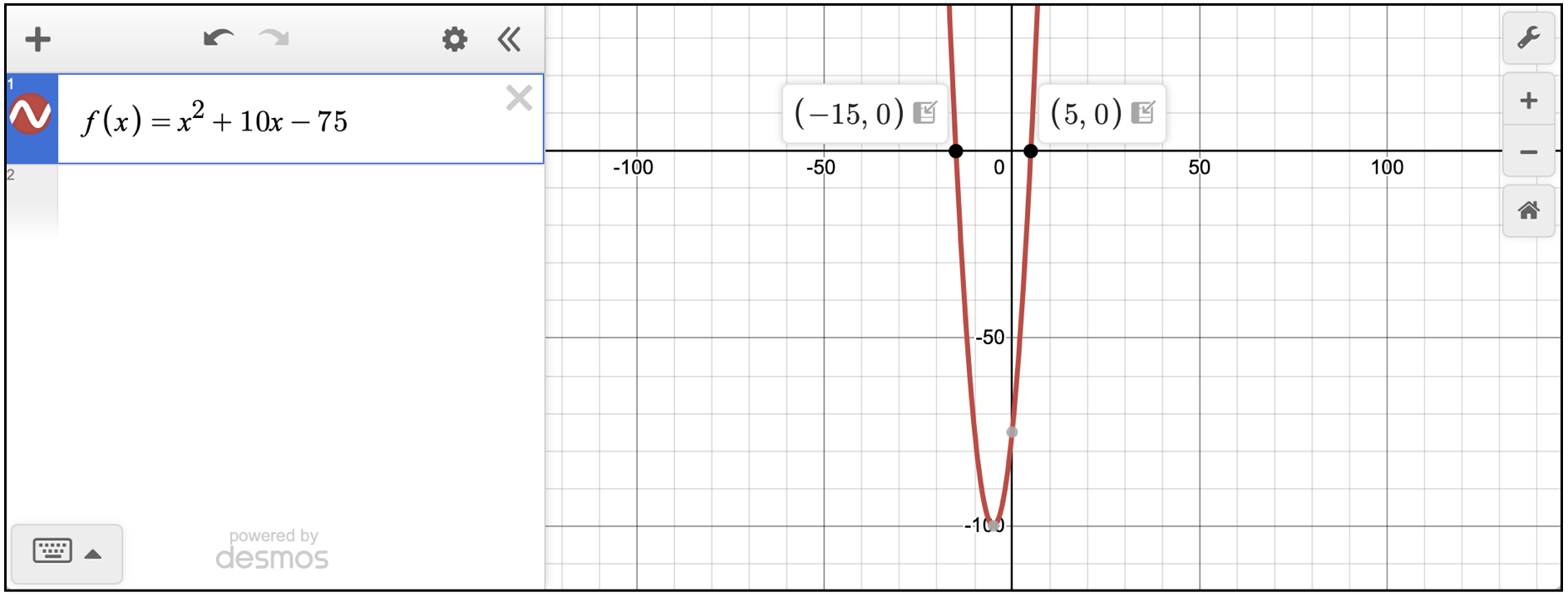
Como ves, los interceptos en x son (-15, 0) y (5, 0). La alternativa correcta es la A.
💡 Recuerda:
✏️ Intercepto en y
Con Álgebra: Sustituye x = 0
Con Desmos: Punto donde la curva cruza el eje de y
✏️ Intercepto en x
Con Álgebra: Sustituye y = 0 o f(x) = 0
Con Desmos: Punto(s) donde la curva cruza el eje de x
🧠 SAT Tip:
Identifica interceptos con Desmos.
Solo escribe la ecuación y toca los puntos donde la curva cruza los ejes de x y/o y.
Evita errores de cálculo y ahorra tiempo.
🎯 Preguntas Comunes SAT Math: Encontrar el máximo o mínimo
Una de las preguntas más comunes en el SAT es sobre el máximo o mínimo de una función — es decir, el punto más alto o más bajo de su gráfica.
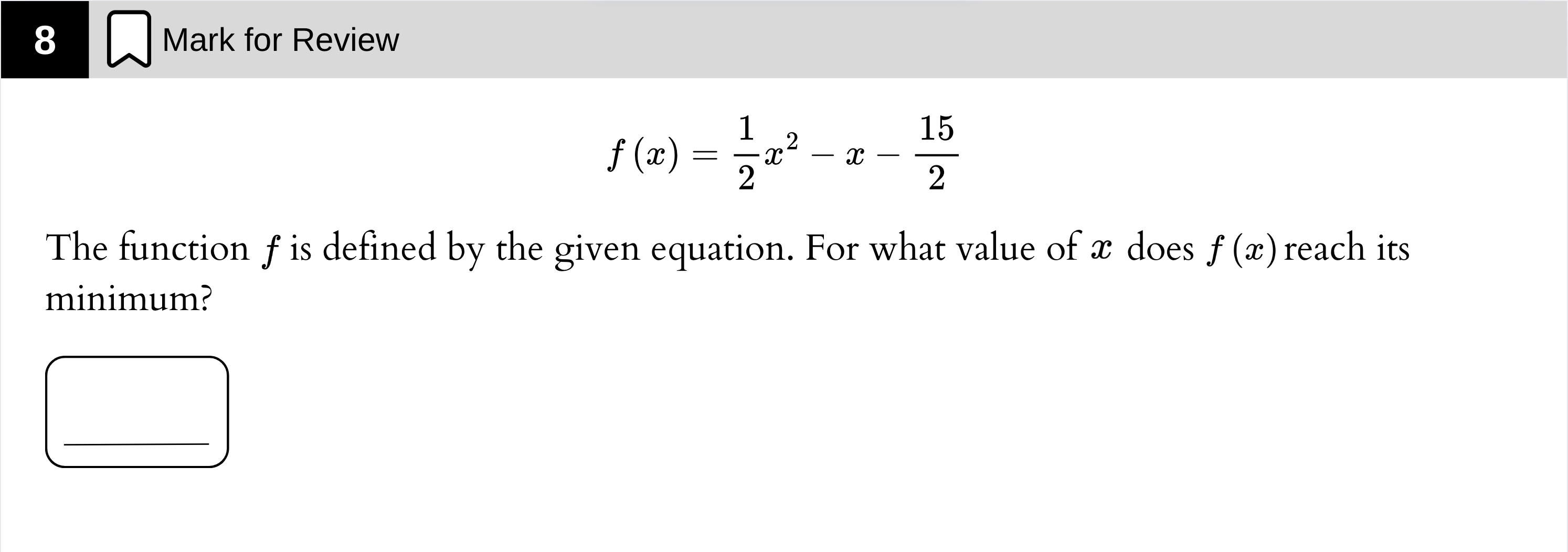
Aunque se puede resolver con álgebra, la forma más sencilla de encontrar el mínimo es observarlo directamente en la gráfica de la función en Desmos.
Así que en esta ocasión, vamos a resolverlo con Desmos primero.
Con Desmos
- Escribe la función original tal como aparece en la pregunta.
- Desmos trazará una parábola. La vértice contiene el punto mínimo.
- Haz clic en la vértice para revelar la coordenada (x, y).
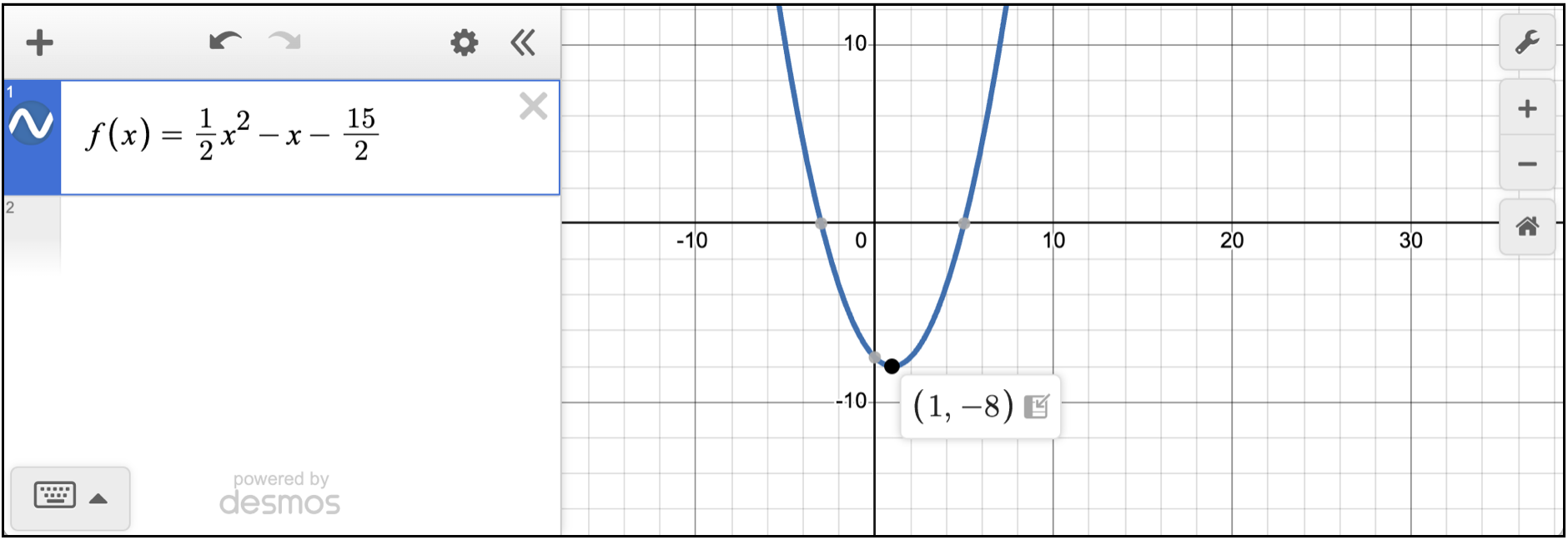
Como te piden el valor de x (“for what value of x”), la contestación correcta es 1.
🧮 Con Álgebra
La función es cuadrática, y con Desmos aprendiste que la gráfica es una parábola y el mínimo está en la vértice.
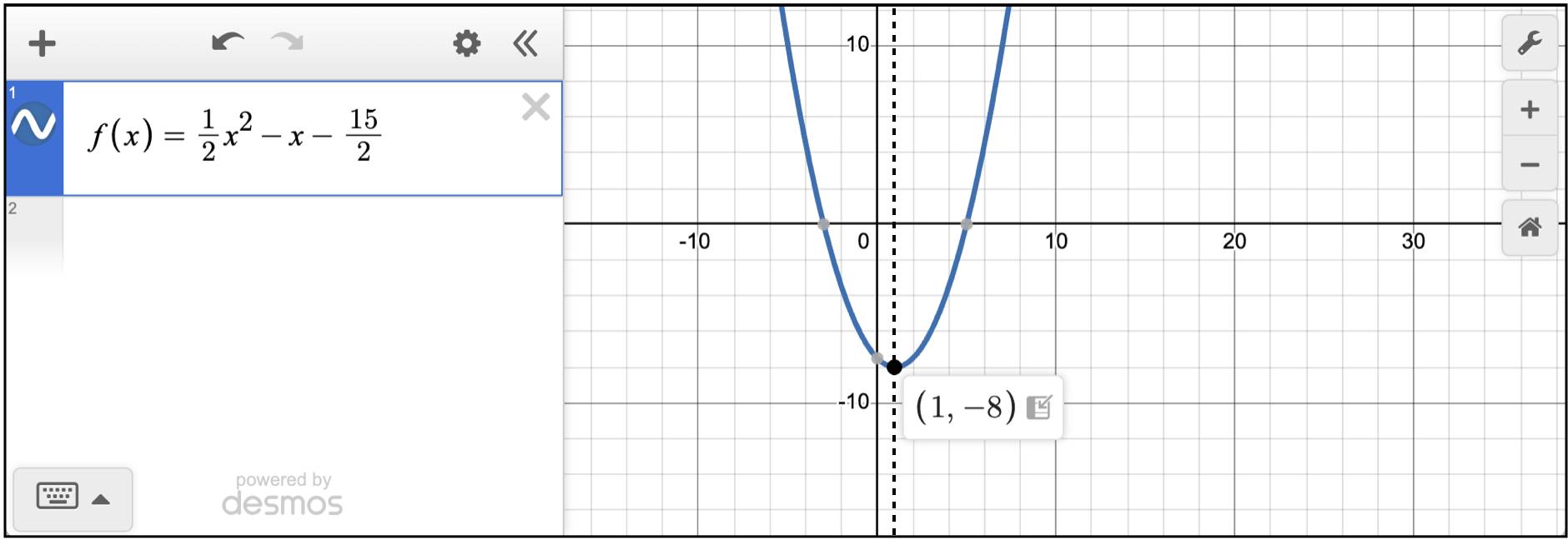
La vértice de una función cuadrática en forma estándar ocurre en el eje de simetría (línea entrecortada).
Como en este caso solo te piden el valor de x (no necesitas el valor de y), basta con calcularlo como sigue:
Como ves, no hay que pasar tanto trabajo. Con Desmos llegas rápidamente a la respuesta.
Ahora veamos un ejemplo en que te pidan un máximo en lugar de un mínimo. El procedimiento en Desmos es el mismo.
🧮 Con Desmos
- Escribe la función original tal como aparece en la pregunta.
- Haz clic en la vértice —el máximo— para revelar la coordenada (x, y).
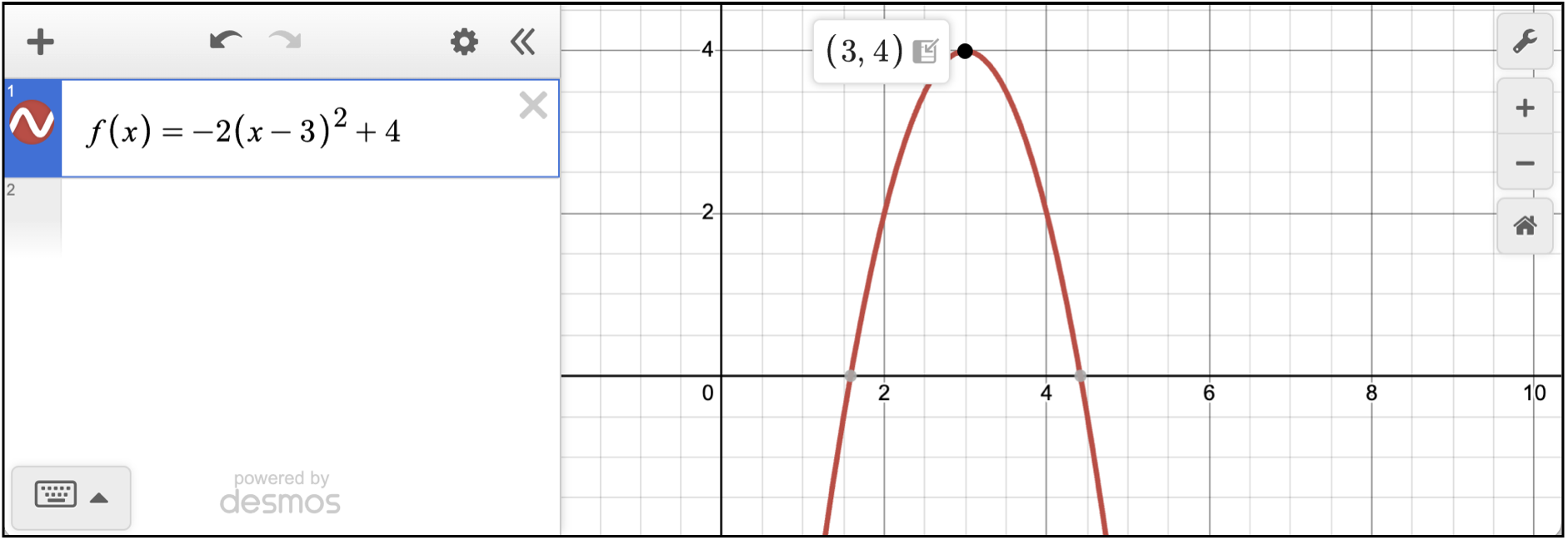
Te piden el valor máximo de la función (“maximum value of the function”). Es decir, te están pidiendo la y de la vértice, no la x.
La vértice es (-3, 4), así que y = 4.
La respuesta correcta es la alternativa D.
🧮 Con Álgebra
En este caso, si conoces el álgebra a continuación, ¡puedes llegar a la respuesta más rápido que con Desmos!
La función cuadrática está escrita en la forma de vértice:
f(x) = a(x − h)2 + k
Donde:
(h, k) es la vértice de la parábola. → ¡Ojo! El valor de h lleva el signo opuesto.
También:
Si a < 0, la parábola abre hacia abajo → la vértice es un máximo (lo que nos piden)
Si a > 0, la parábola abre hacia arriba → la vértice es un mínimo (ver pregunta 8)
En este ejemplo, comparando la función dada con la forma de vértice:
f(x) = a(x − h)2 + k
f(x) = −2(x − 3)2 + 4
Concluimos que:
h = 3 → Cuidado: en la función aparece (x − 3), así que es el opuesto de −3
k = 4 → es el mismo valor que ves en el lugar de k
a = −2 → y como a < 0, la parábola abre hacia abajo (por lo que te piden un máximo)
Como hicimos con Desmos, considera que te están pidiendo el valor máximo de la función. Eso es la y de la vértice, no la x.
En otras palabras, en la vértice (−3, 4), y = 4.
La respuesta correcta es la D.
Como ves, Desmos puede resolver estas preguntas de forma más rápida. 😉
💡 Recuerda:
Si a > 0, la parábola abre hacia arriba → el vértice es un mínimo.
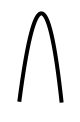Si a < 0, la parábola abre hacia abajo → el vértice es un máximo.
🧠 SAT Tip:
¿Máximos o mínimos? ¡Usa Desmos!
Evita errores que te pueden costar la pregunta.
📚 Lo que sigue en la serie de SAT Math
Las funciones son una parte esencial del SAT Math, y como viste en esta guía, muchas de las preguntas más comunes giran alrededor de los mismos conceptos: evaluar funciones, encontrar interceptos y reconocer el punto máximo o mínimo en una gráfica.
Estas preguntas siempre aparecen en el SAT — así que mientras más las practiques, más puntos tienes asegurados.
Aunque los enunciados cambian, el razonamiento que necesitas es el mismo. Si aprendes a identificar el tipo de pregunta y lo que realmente te están pidiendo, ya tienes la mitad del problema resuelto.
📘 En la próxima parte de esta serie, pasamos al tema de Problem Solving and Data Analysis, donde aprenderás a dominar preguntas de porcientos, promedios, y análisis de datos — una sección donde muchos fallan, pero tú no tienes por qué.
🎓 Prepárate para el SAT con el apoyo de un coach experto y estrategias comprobadas
En Honors Learning Center llevamos más de 30 años ayudando a estudiantes a alcanzar sus metas académicas con programas de preparación que sí funcionan.
Nuestro Honors Review para el SAT es:
✅ Individualizado (1:1)
✅ 100% online — en tiempo real
✅ Bilingüe (español o inglés)
✅ Basado en los temas y preguntas reales del SAT
✅ Enfocado en estrategias probadas y dominio de Desmos, la calculadora integrada en el examen digital
🧠 Te explicamos paso a paso cómo identificar cada tipo de pregunta y te entrenamos con técnicas efectivas para maximizar tu puntuación.
📲 ¿Listo para comenzar? Coordina una consulta por WhatsApp con nuestro equipo académico AQUÍ.
¿Estás listo para alcanzar el éxito académico?
Regístrate ahora y descarga la GUÍA: ¡Descifra el SAT y la PAA! - Las 3 estrategias para las partes de Matemáticas que NECESITAS conocer
No enviamos SPAM. Tu email está seguro con nosotros.
